Material With Highest Specific Heat
In thermodynamics, the specific oestrus capacity (symbol c p ) of a substance is the heat capacity of a sample of the substance divided past the mass of the sample, too sometimes referred to as massic heat capacity. Informally, it is the amount of estrus that must be added to ane unit of mass of the substance in order to crusade an increase of i unit of measurement in temperature. The SI unit of specific oestrus capacity is joule per kelvin per kilogram, J⋅kg−1⋅K−1.[1] For case, the heat required to raise the temperature of 1 kg of h2o by 1 K is 4184 joules, so the specific heat capacity of water is 4184 J⋅kg−ane⋅K−1 .[2]
Specific oestrus capacity oftentimes varies with temperature, and is different for each state of matter. Liquid water has one of the highest specific heat capacities among mutual substances, most 4184 J⋅kg−1⋅K−1 at twenty °C; merely that of ice, just beneath 0 °C, is only 2093 J⋅kg−1⋅K−1 . The specific heat capacities of fe, granite, and hydrogen gas are most 449 J⋅kg−one⋅K−1, 790 J⋅kg−i⋅K−1, and 14300 J⋅kg−1⋅Thousand−1, respectively.[3] While the substance is undergoing a phase transition, such every bit melting or humid, its specific heat capacity is technically infinite, considering the heat goes into changing its state rather than raising its temperature.
The specific heat capacity of a substance, especially a gas, may exist significantly college when it is allowed to expand equally it is heated (specific heat capacity at abiding pressure) than when it is heated in a closed vessel that prevents expansion (specific rut capacity at constant volume). These 2 values are usually denoted past and , respectively; their caliber is the rut chapters ratio.
The term specific heat may also refer to the ratio betwixt the specific rut capacities of a substance at a given temperature and of a reference substance at a reference temperature, such as h2o at xv °C;[4] much in the manner of specific gravity. Specific oestrus chapters is also related to other intensive measures of heat capacity with other denominators. If the amount of substance is measured as a number of moles, i gets the molar heat capacity instead, whose SI unit is joule per kelvin per mole, J⋅mol−1⋅Thousand−one. If the amount is taken to be the book of the sample (as is sometimes done in engineering), ane gets the volumetric rut capacity, whose SI unit is joule per kelvin per cubic meter, J⋅chiliad−3⋅G−ane.
One of the first scientists to use the concept was Joseph Black, an 18th-century medical doctor and professor of medicine at Glasgow Academy. He measured the specific estrus capacities of many substances, using the term chapters for heat.[5]
Definition [edit]
The specific heat capacity of a substance, usually denoted by or s, is the estrus chapters of a sample of the substance, divided by the mass of the sample:[six]
where represents the amount of heat needed to uniformly raise the temperature of the sample past a pocket-size increment .
Like the heat capacity of an object, the specific heat capacity of a substance may vary, sometimes essentially, depending on the starting temperature of the sample and the pressure applied to it. Therefore, it should be considered a function of those two variables.
These parameters are usually specified when giving the specific heat capacity of a substance. For example, "Water (liquid): = 4187 J⋅kg−i⋅One thousand−1 (15 °C)" [7] When not specified, published values of the specific heat capacity generally are valid for some standard weather for temperature and force per unit area.
However, the dependency of on starting temperature and pressure tin can ofttimes be ignored in practical contexts, eastward.g. when working in narrow ranges of those variables. In those contexts one unremarkably omits the qualifier , and approximates the specific estrus chapters by a abiding suitable for those ranges.
Specific rut capacity is an intensive property of a substance, an intrinsic feature that does not depend on the size or shape of the amount in consideration. (The qualifier "specific" in forepart of an extensive property often indicates an intensive property derived from information technology.[8])
Variations [edit]
The injection of heat energy into a substance, besides raising its temperature, usually causes an increase in its book and/or its pressure, depending on how the sample is confined. The choice made near the latter affects the measured specific oestrus chapters, even for the same starting pressure and starting temperature . Two particular choices are widely used:
- If the pressure is kept constant (for instance, at the ambient atmospheric pressure level), and the sample is allowed to expand, the expansion generates work as the force from the pressure displaces the enclosure or the surrounding fluid. That piece of work must come from the heat energy provided. The specific rut chapters thus obtained is said to exist measured at abiding pressure (or isobaric), and is oftentimes denoted , , etc.
- On the other manus, if the expansion is prevented — for instance by a sufficiently rigid enclosure, or past increasing the external pressure to annul the internal one — no work is generated, and the heat energy that would have gone into it must instead contribute to the internal free energy of the sample, including raising its temperature past an extra amount. The specific estrus chapters obtained this way is said to exist measured at abiding book (or isochoric) and denoted , , , etc.
The value of is usually less than the value of . This deviation is peculiarly notable in gases where values under constant pressure are typically xxx% to 66.7% greater than those at constant book. Hence the heat capacity ratio of gases is typically betwixt 1.three and 1.67.[9]
Applicability [edit]
The specific oestrus capacity tin can exist defined and measured for gases, liquids, and solids of adequately general composition and molecular construction. These include gas mixtures, solutions and alloys, or heterogenous materials such as milk, sand, granite, and concrete, if considered at a sufficiently large scale.
The specific heat capacity tin can be defined also for materials that change state or limerick as the temperature and pressure modify, as long as the changes are reversible and gradual. Thus, for example, the concepts are definable for a gas or liquid that dissociates as the temperature increases, as long as the products of the dissociation promptly and completely recombine when information technology drops.
The specific heat capacity is not meaningful if the substance undergoes irreversible chemical changes, or if there is a phase alter, such as melting or boiling, at a sharp temperature within the range of temperatures spanned by the measurement.
Measurement [edit]
The specific heat capacity of a substance is typically determined according to the definition; namely, by measuring the oestrus capacity of a sample of the substance, ordinarily with a calorimeter, and dividing by the sample's mass . Several techniques can be practical for estimating the heat chapters of a substance as for case fast differential scanning calorimetry.[10] [eleven]
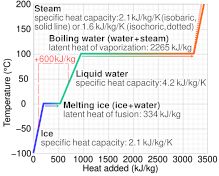
Graph of temperature of phases of h2o heated from −100 °C to 200 °C – the dashed line case shows that melting and heating 1 kg of ice at −l °C to water at xl °C needs 600 kJ
The specific heat capacities of gases tin be measured at abiding volume, by enclosing the sample in a rigid container. On the other hand, measuring the specific heat capacity at constant volume can be prohibitively difficult for liquids and solids, since one often would need impractical pressures in guild to prevent the expansion that would be caused by even pocket-size increases in temperature. Instead, the common practice is to measure the specific heat capacity at constant pressure level (allowing the textile to expand or contract as it wishes), determine separately the coefficient of thermal expansion and the compressibility of the material, and compute the specific rut capacity at abiding volume from these data according to the laws of thermodynamics.[ citation needed ]
Units [edit]
International system [edit]
The SI unit for specific estrus capacity is joule per kelvin per kilogram J / kg⋅K , J⋅M−one⋅kg−1. Since an increase of temperature of ane degree Celsius is the same as an increment of one kelvin, that is the same as joule per degree Celsius per kilogram: J/(kg⋅°C). Sometimes the gram is used instead of kilogram for the unit of measurement of mass: 1 J⋅g−1⋅K−ane = 0.001 J⋅kg−one⋅One thousand−1.
The specific oestrus capacity of a substance (per unit of mass) has dimension Fifty2⋅Θ−1⋅T−2, or (Fifty/T)two/Θ. Therefore, the SI unit J⋅kg−ane⋅Chiliad−i is equivalent to metre squared per second squared per kelvin (m2⋅G−1⋅s−2).
Royal engineering science units [edit]
Professionals in construction, ceremonious engineering, chemical engineering science, and other technical disciplines, peculiarly in the United States, may use English Applied science units including the pound (lb = 0.45359237 kg) as the unit of mass, the degree Fahrenheit or Rankine (°R = five / 9 1000, about 0.555556 K) as the unit of measurement of temperature increment, and the British thermal unit (BTU ≈ 1055.056 J),[12] [13] as the unit of rut.
In those contexts, the unit of specific estrus capacity is BTU/lb⋅°R, or 1 BTU / lb⋅°R = 4186.68 J / kg⋅Thou .[14] The BTU was originally defined so that the average specific heat capacity of water would be 1 BTU/lb⋅°F.[15] Note the value's similarity to that of the calorie - 4187 J/kg⋅°C ≈ 4184 J/kg⋅°C (~.07%) - as they are essentially measuring the same energy, using h2o equally a basis reference, scaled to their systems' respective lbs and °F, or kg and °C.
Calories [edit]
In chemistry, heat amounts were often measured in calories. Confusingly, ii units with that name, denoted "cal" or "Cal", take been ordinarily used to measure out amounts of heat:
- the "small calorie" (or "gram-calorie", "cal") is 4.184 J, exactly. It was originally divers so that the specific estrus capacity of liquid water would exist 1 cal/°C⋅g.
- The "grand calorie" (too "kilocalorie", "kilogram-calorie", or "food calorie"; "kcal" or "Cal") is 1000 pocket-size calories, that is, 4184 J, exactly. It was divers and then that the specific rut capacity of water would be 1 Cal/°C⋅kg.
While these units are notwithstanding used in some contexts (such as kilogram calorie in nutrition), their utilize is now deprecated in technical and scientific fields. When heat is measured in these units, the unit of specific heat capacity is unremarkably
- i cal / °C⋅thousand ("small calorie") = 1 Cal / °C⋅kg = 1 kcal / °C⋅kg ("big calorie") = 4184 J / kg⋅°M [16] = 4.184 kJ / kg⋅°K .
Notation that while cal is 1⁄1000 of a Cal or kcal, information technology is also per gram instead of kilo gram: ergo, in either unit of measurement, the specific heat capacity of water is approximately 1.
Physical basis [edit]
The temperature of a sample of a substance reflects the average kinetic free energy of its constituent particles (atoms or molecules) relative to its center of mass. However, not all energy provided to a sample of a substance will go into raising its temperature, exemplified via the equipartition theorem.
Monatomic gases [edit]
Breakthrough mechanics predicts that, at room temperature and ordinary pressures, an isolated atom in a gas cannot store any significant amount of energy except in the form of kinetic free energy. Thus, heat capacity per mole is the same for all monatomic gases (such as the noble gases). More precisely, and , where is the ideal gas unit of measurement (which is the product of Boltzmann conversion constant from kelvin microscopic energy unit to the macroscopic energy unit joule, and the Avogadro number).
Therefore, the specific rut chapters (per unit of measurement of mass, not per mole) of a monatomic gas will be inversely proportional to its (adimensional) atomic weight . That is, approximately,
For the noble gases, from helium to xenon, these computed values are
| Gas | He | Ne | Ar | Kr | Xe |
|---|---|---|---|---|---|
| four.00 | 20.17 | 39.95 | 83.80 | 131.29 | |
| (J⋅K−1⋅kg−1) | 3118 | 618.3 | 312.two | 148.8 | 94.99 |
| (J⋅G−1⋅kg−1) | 5197 | 1031 | 520.3 | 248.0 | 158.3 |
Polyatomic gases [edit]
On the other mitt, a polyatomic gas molecule (consisting of two or more atoms jump together) can store heat energy in other forms besides its kinetic energy. These forms include rotation of the molecule, and vibration of the atoms relative to its center of mass.
These extra degrees of liberty or "modes" contribute to the specific estrus chapters of the substance. Namely, when heat energy is injected into a gas with polyatomic molecules, simply part of information technology volition go into increasing their kinetic energy, and hence the temperature; the residue will get to into those other degrees of freedom. In social club to achieve the same increase in temperature, more heat energy will have to exist provided to a mol of that substance than to a mol of a monatomic gas. Therefore, the specific heat capacity of a polyatomic gas depends not merely on its molecular mass, but besides on the number of degrees of freedom that the molecules take.[17] [18] [xix]
Quantum mechanics farther says that each rotational or vibrational way can only take or lose energy in certain discrete amount (quanta). Depending on the temperature, the average heat energy per molecule may be too small compared to the quanta needed to activate some of those degrees of liberty. Those modes are said to be "frozen out". In that case, the specific heat chapters of the substance is going to increment with temperature, sometimes in a pace-similar style, as more modes become unfrozen and start absorbing role of the input heat energy.
For example, the molar oestrus chapters of nitrogen N
ii at abiding volume is (at 15 °C, 1 atm), which is .[20] That is the value expected from theory if each molecule had v degrees of freedom. These plough out to be three degrees of the molecule'south velocity vector, plus two degrees from its rotation well-nigh an centrality through the middle of mass and perpendicular to the line of the ii atoms. Because of those ii actress degrees of freedom, the specific heat chapters of Northward
2 (736 J⋅G−1⋅kg−1) is greater than that of an hypothetical monatomic gas with the aforementioned molecular mass 28 (445 J⋅K−1⋅kg−1), by a factor of five / 3 .
This value for the specific heat capacity of nitrogen is practically constant from beneath −150 °C to about 300 °C. In that temperature range, the 2 boosted degrees of freedom that represent to vibrations of the atoms, stretching and compressing the bond, are still "frozen out". At about that temperature, those modes brainstorm to "un-freeze", and every bit a consequence starts to increase apace at first, then slower as it tends to another constant value. Information technology is 35.five J⋅Thousand−one⋅mol−one at 1500 °C, 36.9 at 2500 °C, and 37.5 at 3500 °C.[21] The last value corresponds near exactly to the predicted value for 7 degrees of freedom per molecule.
Derivations of heat capacity [edit]
Relation between specific heat capacities [edit]
Starting from the cardinal thermodynamic relation one can show,
where,
A derivation is discussed in the commodity Relations betwixt specific heats.
For an ideal gas, if is expressed as molar density in the higher up equation, this equation reduces simply to Mayer'south relation,
where and are intensive belongings heat capacities expressed on a per mole footing at constant pressure level and abiding volume, respectively.
Specific oestrus capacity [edit]
The specific heat capacity of a material on a per mass basis is
which in the absenteeism of phase transitions is equivalent to
where
For gases, and also for other materials under high pressures, in that location is need to distinguish between different boundary conditions for the processes under consideration (since values differ significantly between different atmospheric condition). Typical processes for which a heat capacity may be defined include isobaric (constant pressure, ) or isochoric (constant volume, ) processes. The corresponding specific heat capacities are expressed as
A related parameter to is , the volumetric heat capacity. In engineering practice, for solids or liquids often signifies a volumetric heat capacity, rather than a constant-book ane. In such cases, the mass-specific rut capacity is frequently explicitly written with the subscript , as . Of class, from the to a higher place relationships, for solids 1 writes
For pure homogeneous chemical compounds with established molecular or molar mass or a molar quantity is established, heat capacity equally an intensive holding tin can be expressed on a per mole basis instead of a per mass ground by the following equations analogous to the per mass equations:
where north = number of moles in the body or thermodynamic organization. Ane may refer to such a per mole quantity as molar estrus chapters to distinguish information technology from specific heat chapters on a per-mass basis.
Polytropic heat capacity [edit]
The polytropic heat capacity is calculated at processes if all the thermodynamic properties (pressure, volume, temperature) change
The most of import polytropic processes run betwixt the adiabatic and the isotherm functions, the polytropic alphabetize is between one and the adiabatic exponent (γ or κ)
Dimensionless heat capacity [edit]
The dimensionless heat capacity of a fabric is
where
- C is the heat capacity of a body fabricated of the material in question (J/Thousand)
- due north is the corporeality of substance in the body (mol)
- R is the gas constant (J⋅Grand−one⋅mol−i)
- N is the number of molecules in the body. (dimensionless)
- k B is the Boltzmann constant (J⋅K−1)
Over again, SI units shown for instance.
Read more than about the quantities of dimension ane[22] at BIPM
In the Platonic gas article, dimensionless estrus capacity is expressed as .
Rut chapters at absolute zero [edit]
From the definition of entropy
the absolute entropy can exist calculated by integrating from naught kelvins temperature to the terminal temperature Tf
The heat capacity must be zero at cipher temperature in order for the above integral not to yield an infinite accented entropy, thus violating the third law of thermodynamics. One of the strengths of the Debye model is that (unlike the preceding Einstein model) information technology predicts the proper mathematical form of the arroyo of heat capacity toward nil, as absolute null temperature is approached.
Solid phase [edit]
The theoretical maximum heat capacity for larger and larger multi-atomic gases at higher temperatures, as well approaches the Dulong–Petit limit of 3R, and so long as this is calculated per mole of atoms, non molecules. The reason is that gases with very large molecules, in theory take near the same high-temperature heat chapters equally solids, lacking only the (minor) heat capacity contribution that comes from potential free energy that cannot be stored between separate molecules in a gas.
The Dulong–Petit limit results from the equipartition theorem, and equally such is only valid in the classical limit of a microstate continuum, which is a loftier temperature limit. For calorie-free and non-metallic elements, as well as most of the common molecular solids based on carbon compounds at standard ambience temperature, quantum effects may also play an important role, as they practise in multi-atomic gases. These furnishings usually combine to requite heat capacities lower than iiiR per mole of atoms in the solid, although in molecular solids, rut capacities calculated per mole of molecules in molecular solids may be more than than 3R. For example, the rut chapters of water ice at the melting point is most 4.6R per mole of molecules, but merely 1.5R per mole of atoms. The lower than iiiR number "per atom" (as is the case with diamond and beryllium) results from the "freezing out" of possible vibration modes for light atoms at suitably low temperatures, just as in many low-mass-atom gases at room temperatures. Because of high crystal binding energies, these effects are seen in solids more often than liquids: for example the rut capacity of liquid water is twice that of ice at virtually the same temperature, and is again close to the threeR per mole of atoms of the Dulong–Petit theoretical maximum.
For a more mod and precise analysis of the heat capacities of solids, especially at low temperatures, it is useful to use the thought of phonons. Run across Debye model.
Theoretical estimation [edit]
The path integral Monte Carlo method is a numerical approach for determining the values of heat capacity, based on quantum dynamical principles. However, good approximations can be made for gases in many states using simpler methods outlined below. For many solids composed of relatively heavy atoms (atomic number > fe), at not-cryogenic temperatures, the heat capacity at room temperature approaches 3R = 24.94 joules per kelvin per mole of atoms (Dulong–Petit constabulary, R is the gas constant). Low temperature approximations for both gases and solids at temperatures less than their feature Einstein temperatures or Debye temperatures can exist made by the methods of Einstein and Debye discussed below. Water (liquid): CP = 4185.5 J⋅K−1⋅kg−1 (xv °C, 101.325 kPa) Water (liquid): CVH = 74.539 J⋅K−ane⋅mol−1 (25 °C) For liquids and gases, information technology is of import to know the pressure to which given rut capacity data refer. Most published data are given for standard pressure. However, unlike standard conditions for temperature and force per unit area have been divers past different organizations. The International Marriage of Pure and Applied Chemical science (IUPAC) inverse its recommendation from one atmosphere to the round value 100 kPa (≈750.062 Torr).[notes ane]
Calculation from first principles [edit]
The path integral Monte Carlo method is a numerical approach for determining the values of heat capacity, based on breakthrough dynamical principles. Yet, skilful approximations tin can be made for gases in many states using simpler methods outlined beneath. For many solids composed of relatively heavy atoms (atomic number > atomic number 26), at not-cryogenic temperatures, the heat chapters at room temperature approaches 3R = 24.94 joules per kelvin per mole of atoms (Dulong–Petit law, R is the gas constant). Low temperature approximations for both gases and solids at temperatures less than their characteristic Einstein temperatures or Debye temperatures tin can exist made by the methods of Einstein and Debye discussed below.
Relation between estrus capacities [edit]
Measuring the specific heat capacity at constant book can exist prohibitively difficult for liquids and solids. That is, small temperature changes typically require large pressures to maintain a liquid or solid at constant volume, implying that the containing vessel must be nearly rigid or at least very strong (see coefficient of thermal expansion and compressibility). Instead, it is easier to measure the heat capacity at constant force per unit area (allowing the textile to expand or contract freely) and solve for the estrus capacity at constant book using mathematical relationships derived from the basic thermodynamic laws.
The heat capacity ratio, or adiabatic alphabetize, is the ratio of the rut capacity at constant pressure to heat capacity at constant book. Information technology is sometimes too known every bit the isentropic expansion factor.
Ideal gas [edit]
[23] For an ideal gas, evaluating the partial derivatives higher up according to the equation of state, where R is the gas constant, for an ideal gas
Substituting
this equation reduces just to Mayer's relation:
The differences in heat capacities as defined by the in a higher place Mayer relation is only exact for an ideal gas and would be different for any real gas.
Specific rut capacity [edit]
The specific heat chapters of a material on a per mass footing is
which in the absence of phase transitions is equivalent to
where
For gases, and too for other materials under high pressures, there is need to distinguish between different boundary conditions for the processes under consideration (since values differ significantly betwixt unlike conditions). Typical processes for which a rut capacity may be divers include isobaric (constant pressure, ) or isochoric (constant book, ) processes. The corresponding specific estrus capacities are expressed every bit
From the results of the previous section, dividing through by the mass gives the relation
A related parameter to is , the volumetric rut capacity. In engineering do, for solids or liquids oftentimes signifies a volumetric oestrus capacity, rather than a constant-volume one. In such cases, the specific heat capacity is often explicitly written with the subscript , every bit . Of class, from the to a higher place relationships, for solids one writes
For pure homogeneous chemical compounds with established molecular or molar mass, or a molar quantity, heat capacity as an intensive belongings can be expressed on a per-mole basis instead of a per-mass basis by the following equations analogous to the per mass equations:
where northward is the number of moles in the torso or thermodynamic arrangement. One may refer to such a per-mole quantity as molar estrus capacity to distinguish it from specific heat capacity on a per-mass basis.
Polytropic heat chapters [edit]
The polytropic oestrus capacity is calculated at processes if all the thermodynamic properties (pressure, volume, temperature) alter:
The most of import polytropic processes run between the adiabatic and the isotherm functions, the polytropic alphabetize is between 1 and the adiabatic exponent (γ or κ).
Dimensionless heat capacity [edit]
The dimensionless rut capacity of a material is
where
- is the rut chapters of a body fabricated of the material in question (J/1000),
- n is the amount of substance in the body (mol),
- R is the gas constant (J/(K⋅mol)),
- Northward is the number of molecules in the body (dimensionless),
- k B is the Boltzmann abiding (J/(1000⋅molecule)).
In the platonic gas article, dimensionless heat capacity is expressed as and is related in that location direct to half the number of degrees of freedom per particle. This holds true for quadratic degrees of freedom, a consequence of the equipartition theorem.
More generally, the dimensionless heat capacity relates the logarithmic increase in temperature to the increase in the dimensionless entropy per particle , measured in nats.
Alternatively, using base-2 logarithms, relates the base of operations-2 logarithmic increase in temperature to the increase in the dimensionless entropy measured in bits.[24]
Heat capacity at absolute nix [edit]
From the definition of entropy
the absolute entropy can exist calculated past integrating from zero to the last temperature T f:
Thermodynamic derivation [edit]
In theory, the specific estrus capacity of a substance tin also be derived from its abstract thermodynamic modeling by an equation of state and an internal energy function.
State of matter in a homogeneous sample [edit]
To apply the theory, 1 considers the sample of the substance (solid, liquid, or gas) for which the specific oestrus chapters can exist defined; in detail, that it has homogeneous limerick and fixed mass . Assume that the evolution of the system is e'er wearisome enough for the internal pressure level and temperature be considered uniform throughout. The pressure would be equal to the pressure level applied to it by the enclosure or some surrounding fluid, such every bit air.
The state of the material can then be specified by three parameters: its temperature , the force per unit area , and its specific book , where is the volume of the sample. (This quantity is the reciprocal of the material'southward density .) Like and , the specific volume is an intensive property of the material and its state, that does not depend on the amount of substance in the sample.
Those variables are not independent. The allowed states are defined past an equation of state relating those three variables: The function depends on the cloth nether consideration. The specific internal free energy stored internally in the sample, per unit of mass, volition and then be some other function of these country variables, that is likewise specific of the material. The total internal energy in the sample so will be .
For some unproblematic materials, like an platonic gas, ane can derive from bones theory the equation of land and even the specific internal energy In general, these functions must be determined experimentally for each substance.
Conservation of energy [edit]
The absolute value of this quantity is undefined, and (for the purposes of thermodynamics) the state of "nil internal energy" tin can be chosen arbitrarily. However, past the law of conservation of energy, any infinitesimal increase in the total internal energy must be matched by the cyberspace menstruum of heat energy into the sample, plus whatever internet mechanical energy provided to it by enclosure or surrounding medium on it. The latter is , where is the change in the sample's volume in that infinitesimal step.[25] Therefore
hence
If the volume of the sample (hence the specific volume of the material) is kept constant during the injection of the heat corporeality , then the term is zero (no mechanical piece of work is done). Then, dividing by ,
where is the modify in temperature that resulted from the estrus input. The left-hand side is the specific heat capacity at constant volume of the material.
For the heat capacity at abiding pressure, it is useful to define the specific enthalpy of the organisation as the sum . An infinitesimal alter in the specific enthalpy will then be
therefore
If the pressure is kept constant, the 2d term on the left-hand side is nil, and
The left-hand side is the specific oestrus chapters at constant pressure of the cloth.
Connection to equation of land [edit]
In full general, the minute quantities are constrained by the equation of country and the specific internal free energy function. Namely,
Here denotes the (partial) derivative of the state equation with respect to its argument, keeping the other two arguments stock-still, evaluated at the country in question. The other partial derivatives are defined in the same way. These 2 equations on the four infinitesimal increments usually constrain them to a two-dimensional linear subspace space of possible infinitesimal state changes, that depends on the cloth and on the state. The constant-volume and abiding-pressure changes are but two particular directions in this space.
This assay as well holds no matter how the energy increment is injected into the sample, namely by heat conduction, irradiation, electromagnetic induction, radioactive disuse, etc.
Relation between heat capacities [edit]
For any specific volume , announce the part that describes how the pressure varies with the temperature , as immune by the equation of country, when the specific volume of the fabric is forcefully kept constant at . Analogously, for any pressure level , let exist the part that describes how the specific book varies with the temperature, when the force per unit area is kept abiding at . Namely, those functions are such that
and
for any values of . In other words, the graphs of and are slices of the surface defined by the state equation, cut by planes of constant and abiding , respectively.
And then, from the fundamental thermodynamic relation it follows that
This equation can be rewritten as
where
both depending on the state .
The heat capacity ratio, or adiabatic alphabetize, is the ratio of the estrus capacity at constant force per unit area to heat capacity at constant book. It is sometimes also known equally the isentropic expansion factor.
Calculation from first principles [edit]
The path integral Monte Carlo method is a numerical approach for determining the values of heat capacity, based on quantum dynamical principles. All the same, good approximations can be made for gases in many states using simpler methods outlined below. For many solids composed of relatively heavy atoms (atomic number > atomic number 26), at not-cryogenic temperatures, the rut capacity at room temperature approaches 3R = 24.94 joules per kelvin per mole of atoms (Dulong–Petit law, R is the gas constant). Depression temperature approximations for both gases and solids at temperatures less than their characteristic Einstein temperatures or Debye temperatures can be fabricated by the methods of Einstein and Debye discussed beneath. Still, attending should exist fabricated for the consistency of such ab-initio considerations when used along with an equation of state for the considered material.[26]
Ideal gas [edit]
For an ideal gas, evaluating the fractional derivatives higher up according to the equation of state, where R is the gas constant, for an ideal gas[27]
Substituting
this equation reduces merely to Mayer's relation:
The differences in heat capacities as defined by the to a higher place Mayer relation is only verbal for an ideal gas and would be different for whatsoever real gas.
Encounter also [edit]
![]() Physics portal
Physics portal
- Specific heat of melting (Enthalpy of fusion)
- Specific heat of vaporization (Enthalpy of vaporization)
- Frenkel line
- Heat capacity ratio
- Heat equation
- Rut transfer coefficient
- History of thermodynamics
- Joback method (Estimation of estrus capacities)
- Latent heat
- Material properties (thermodynamics)
- Quantum statistical mechanics
- R-value (insulation)
- Specific rut of vaporization
- Specific melting heat
- Statistical mechanics
- Tabular array of specific estrus capacities
- Thermal mass
- Thermodynamic databases for pure substances
- Thermodynamic equations
- Volumetric heat chapters
Notes [edit]
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Standard Pressure". doi:10.1351/goldbook.S05921.
References [edit]
- ^ Open University (2008). S104 Book iii Energy and Light, p. 59. The Open University. ISBN 9781848731646.
- ^ Open Academy (2008). S104 Book iii Energy and Calorie-free, p. 179. The Open University. ISBN 9781848731646.
- ^ Engineering ToolBox (2003). "Specific Estrus of some common Substances".
- ^ (2001): Columbia Encyclopedia, 6th ed.; as quoted by Encyclopedia.com. Columbia University Printing. Accessed on 2019-04-xi.
- ^ Laidler, Keith, J. (1993). The World of Concrete Chemistry. Oxford University Press. ISBN0-xix-855919-4.
- ^ International Agency of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN92-822-2213-six, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- ^ "Water – Thermal Properties". Engineeringtoolbox.com. Retrieved 2021-03-29 .
- ^ International Union of Pure and Practical Chemistry, Concrete Chemical science Sectionalisation. "Quantities, Units and Symbols in Physical Chemistry" (PDF). Blackwell Sciences. p. 7.
The adjective specific before the proper noun of an extensive quantity is often used to mean divided by mass.
- ^ Lange's Handbook of Chemistry, tenth ed. page 1524
- ^ Quick, C. R.; Schawe, J. E. Thousand.; Uggowitzer, P. J.; Pogatscher, S. (2019-07-01). "Measurement of specific estrus capacity via fast scanning calorimetry—Accurateness and loss corrections". Thermochimica Acta. Special Issue on occasion of the 65th birthday of Christoph Schick. 677: 12–20. doi:10.1016/j.tca.2019.03.021. ISSN 0040-6031.
- ^ Pogatscher, South.; Leutenegger, D.; Schawe, J. E. K.; Uggowitzer, P. J.; Löffler, J. F. (September 2016). "Solid–solid stage transitions via melting in metals". Nature Communications. seven (1): 11113. Bibcode:2016NatCo...711113P. doi:10.1038/ncomms11113. ISSN 2041-1723. PMC4844691. PMID 27103085.
- ^ Koch, Werner (2013). VDI Steam Tables (4 ed.). Springer. p. viii. ISBN9783642529412. Published under the auspices of the Verein Deutscher Ingenieure (VDI).
- ^ Cardarelli, Francois (2012). Scientific Unit of measurement Conversion: A Practical Guide to Metrication. Thou.J. Shields (translation) (2 ed.). Springer. p. 19. ISBN9781447108054.
- ^ From straight values: 1 BTU / lb⋅°R × 1055.06 J / BTU × ( 1 / 0.45359237 ) lb / kg x 9 / 5 °R / Thousand = 4186.82 J / kg⋅K
- ^ °F=°R
- ^ °C=°K
- ^ Feynman, R., The Feynman Lectures on Physics, Vol. 1, ch. 40, pp. 7–8
- ^ Reif, F. (1965). Fundamentals of statistical and thermal physics . McGraw-Hill. pp. 253–254.
- ^ Kittel, Charles and Kroemer, Herbert (2000). Thermal physics. Freeman. p. 78. ISBN978-0-7167-1088-two.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Thornton, Steven T. and Rex, Andrew (1993) Modern Physics for Scientists and Engineers, Saunders College Publishing
- ^ Chase, Grand.W. Jr. (1998) NIST-JANAF Themochemical Tables, Fourth Edition, In Journal of Physical and Chemical Reference Information, Monograph 9, pages 1–1951.
- ^ "About the unit of measurement one".
- ^ Yunus A. Cengel and Michael A. Boles,Thermodynamics: An Engineering Approach, 7th Edition, McGraw-Hill, 2010, ISBN 007-352932-X.
- ^ Fraundorf, P. (2003). "Estrus chapters in bits". American Journal of Physics. 71 (eleven): 1142. arXiv:cond-mat/9711074. Bibcode:2003AmJPh..71.1142F. doi:10.1119/i.1593658. S2CID 18742525.
- ^ Feynman, Richard The Feynman Lectures on Physics, Vol. 1, Ch. 45
- ^ South. Benjelloun, "Thermodynamic identities and thermodynamic consistency of Equation of States", Link to Archiv e-print Link to Hal e-print
- ^ Cengel, Yunus A. and Boles, Michael A. (2010) Thermodynamics: An Engineering science Approach, 7th Edition, McGraw-Loma ISBN 007-352932-X.
Further reading [edit]
- Emmerich Wilhelm & Trevor Thou. Letcher, Eds., 2010, Heat Capacities: Liquids, Solutions and Vapours, Cambridge, U.Thousand.:Royal Order of Chemistry, ISBN 0-85404-176-1. A very recent outline of selected traditional aspects of the title subject, including a recent specialist introduction to its theory, Emmerich Wilhelm, "Estrus Capacities: Introduction, Concepts, and Selected Applications" (Chapter 1, pp. 1–27), chapters on traditional and more contemporary experimental methods such as photoacoustic methods, e.g., Jan Thoen & Christ Glorieux, "Photothermal Techniques for Heat Capacities," and chapters on newer research interests, including on the heat capacities of proteins and other polymeric systems (Chs. 16, xv), of liquid crystals (Ch. 17), etc.
External links [edit]
- (2012-05may-24) Phonon theory sheds light on liquid thermodynamics, rut chapters – Physics World The phonon theory of liquid thermodynamics | Scientific Reports
Material With Highest Specific Heat,
Source: https://en.wikipedia.org/wiki/Specific_heat_capacity
Posted by: daughertyvittlentoond1970.blogspot.com































































































![{\displaystyle {\begin{cases}\displaystyle \mathrm {d} T{\frac {\partial F}{\partial T}}(T,P,V)+\mathrm {d} P{\frac {\partial F}{\partial P}}(T,P,V)+\mathrm {d} V{\frac {\partial F}{\partial V}}(T,P,V)&=&0\\[2ex]\displaystyle \mathrm {d} T{\frac {\partial U}{\partial T}}(T,P,V)+\mathrm {d} P{\frac {\partial U}{\partial P}}(T,P,V)+\mathrm {d} V{\frac {\partial U}{\partial V}}(T,P,V)&=&\mathrm {d} U\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/957c9a178ff753bc04a30bed2819d7e5155314a0)







![{\displaystyle c_{P}(T,P,\nu )-c_{V}(T,P,\nu )=T\left[{\frac {\mathrm {d} p_{\nu }}{\mathrm {d} T}}(T)\right]\left[{\frac {\mathrm {d} \nu _{P}}{\mathrm {d} T}}(T)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24554d2ae7d16cbb75b6ad485bf92856b55cf7bd)




0 Response to "Material With Highest Specific Heat"
Post a Comment