Utility Function For Perfect Complements

12.4 Examples

Learning Objective

Are there whatever user-friendly functional forms for analyzing consumer option?

The Cobb-Douglas utility part comes in the grade $u (x, y) = x^{α} y^{1 - α} .$ Since utility is zilch if either of the appurtenances is zippo, we run into that a consumer with Cobb-Douglas preferences will always buy some of each good. The marginal rate of substitution for Cobb-Douglas utility is

${- \frac{d y}{d x} |}_{u = u_{0}} = \frac{\frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}} = \frac{α y}{(1 - α) x} .$

Thus, the consumer'south utility maximization trouble yields

${\frac{p_{X}}{p_{Y}} = - \frac{d y}{d ten} |}_{u = u_{0}} = \frac{\frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}} = \frac{α y}{(1 - α) 10} .$

Thus, using the budget constraint, $(one - α) x p_{10} = α y p_{Y} = α (M - x p_{Ten}) .$ This yields

$ten = \frac{α Chiliad}{p_{X}}, y = \frac{(ane - α) Chiliad}{p_{Y}} .$

The Cobb-Douglas utility results in constant expenditure shares. No matter what the cost of 10 or Y, the expenditure xpX on X is αM. Similarly, the expenditure on Y is (1 – α)M. This makes the Cobb-Douglas utility very useful for computing examples and homework exercises.

When ii appurtenances are perfect complements, they are consumed proportionately. The utility that gives rise to perfect complements is in the form u(x, y) = min {ten, βy} for some constant β (the Greek letter "beta"). First observe that, with perfect complements, consumers will buy in such a style that ten = βy. The reason is that, if x > βy, some expenditure on x is a waste material since it brings in no additional utility; and the consumer gets higher utility by decreasing x and increasing y. This lets us define a "composite good" that involves ownership some amount y of Y and too buying βy of X. The price of this blended commodity is βpX + pY, and it produces utility $u = \frac{M}{β p_{X} + p_{Y}} .$ In this way, perfect complements boil downward to a single practiced problem.

If the only two appurtenances available in the world were pizza and beer, it is likely that satiationThe point at which increased consumption does not increase utility. —the betoken at which increased consumption does not increment utility—would set in at some betoken. How many pizzas can you swallow per month? How much beer tin you potable? (Don't answer that.)

Effigy 12.8 Isoquants for a bliss point

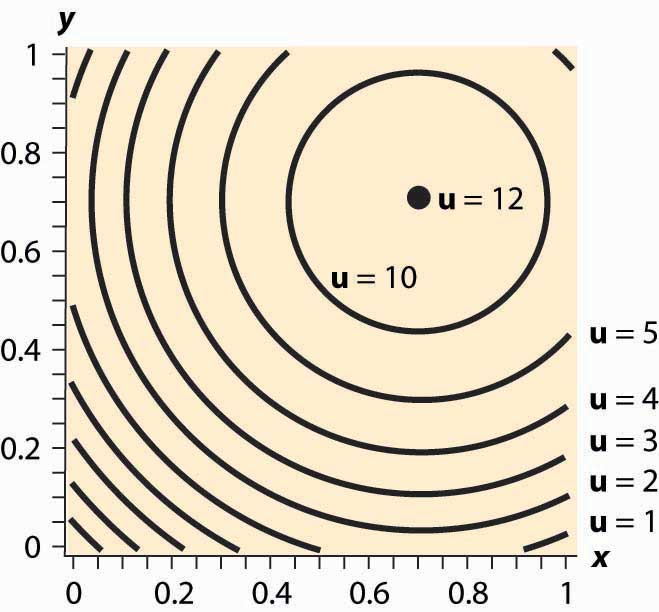
What does satiation mean for isoquants? It means there is a point that maximizes utility, which economists call a bliss pointA signal that maximizes utility. . An example is illustrated in Figure 12.8 "Isoquants for a elation betoken". Near the origin, the isoquants comport equally earlier. However, as ane gets total of pizza and beer, a bespeak of maximum value is reached, illustrated by a big black dot. What does satiation mean for the theory? Commencement, if the bliss point isn't within reach, the theory behaves every bit before. With a bliss point within reach, consumption will finish at the bliss point. A feasible elation point entails having a zero value of money. There may be people with a zero value of money, but even very wealthy people, who reach satiation in goods that they personally swallow, often like to do other things with the wealth and appear not to have reached satiation overall.

Key Takeaways

The Cobb-Douglas utility results in constant expenditure shares.
When two goods are perfect complements, they are consumed proportionately. Perfect complements eddy down to a single proficient problem.
A bliss point, or satiation, is a point at which further increases in consumption reduce utility.

Exercises

Consider a consumer with utility $u (x, y) = \sqrt{x y} .$ If the consumer has $100 to spend, and the price of 10 is $5 and the price of Y is $ii, graph the budget line; and and so detect the point that maximizes the consumer's utility given the budget. Draw the utility isoquant through this point. What are the expenditure shares?
Consider a consumer with utility $u (x, y) = \sqrt{x y} .$ Calculate the gradient of the isoquant directly past solving $u (x, y) = u_{0}$ for y as a role of x and the utility level u ₀. What is the slope ${- \frac{d y}{d x} |}_{u = u_{0}} ?$ Verify that information technology satisfies the formula given above.
Consider a consumer with utility $u (x, y) = {(x y)}^{2} .$ Calculate the slope of the isoquant directly by solving $u (10, y) = u_{0}$ for y equally a function of x and the utility level u ₀. What is the slope ${- \frac{d y}{d x} |}_{u = u_{0}} ?$ Verify that the consequence is the aforementioned as in the previous exercise. Why is it the same?
The case of perfect substitutes arises when all that matters to the consumer is the sum of the products—for example, ruby-red shirts and light-green shirts for a colorblind consumer. In this case, u(x, y) = ten + y. Graph the isoquants for perfect substitutes. Show that the consumer maximizes utility by spending his or her entire income on whichever product is cheaper.
Suppose $u (x, y) = x^{α} + y^{α}$ for α < 1. Show that $x = \frac{M}{p_{X} (one + {(\frac{p_{Y}}{p_{10}})}^{α})}$ and $y = \frac{Yard}{p_{Y} (1 + {(\frac{p_{X}}{p_{Y}})}^{α})} .$
Suppose that ane consumer has the utility function u (which is always a positive number), and a second consumer has utility w. Suppose, in add-on, that for whatever x, y, w(x, y) = (u(10, y))ⁱⁱ; that is, the 2nd person's utility is the square of the kickoff person's. Show that these consumers make the aforementioned choices—that is, u ≥ x_a, y_a ) ≥ u(x_b, y_b ) if and only if w(ten_a, y_a ) ≥ w(x_b, y_b ).